Step 1: Dispersion.

Dispersion is the word used when waves with different frequencies travel with different speeds. Dispersion is most prominent in surface waves. Surface waves of different frequencies are sensitive to structure at different depths. Since the velocity changes as a function of depth, the different frequencies will have different speeds. When there is dispersion, the phase- and the group velocity of a wave are different.
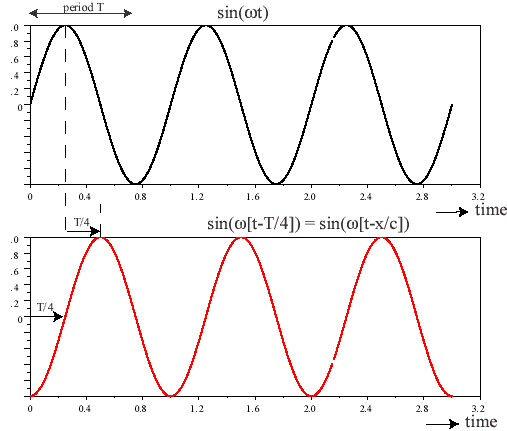
The phase velocity is the speed with which a surface of equal phase (a
wavefront) propagates. It is the propagation velocity of a single frequency component. To recall what we mean by phase, consider a simple sine function (Figure
1). In the top panel, the sine starts at 0 at t = 0s, in the bottom panel, the sine function is
shifted to the right by a quarter of its period. We describe the function in
the top panel as f(t) = sin(wt) where w = angular frequency = 2p f and f is frequency in
Herz. The period of this wave is 2p/w
seconds. If, for example, w = 4p, then T =
0.5 seconds. The function in the bottom panel is f(t) = sin(w(t -
T/4)).
All the points of the signal in the bottom panel are shifted compared to the points with the same
phase in the top panel. Therefore, the bottom panel has a phase shift compared to the upper
panel.
1.The signals in Figure 1 have a period of 1 s.
What is the frequency?
What is the angular frequency?
2.Suppose that the two panels represent seismograms at two different
stations. The distance between the stations is x km, and the speed (phase velocity) of the wave is c. Then the bottom panel can be described as u(x,t) = sin(w[t - x/c]).
You probably have seen the following way of writing this:
u(x,t) = sin(wt - kx), k is called the wave number. If the phase
velocity is 3 km/s, determine what the wave number is.
3.The wavelength is the 'period' in the spatial domain, that is, the
length along x of one period of the wave in km. Determine this sine-wave's
wavelength.
Paragraph 2.8.1 of the textbook shows that if you add two signals (e.g. sines or cosines) that have almost the same frequency and wavenumber, that the resulting wave looks like a wavepacket. A wavepacket travels with the group velocity for the center frequency of the packet. The group velocity is the propagation velocity of energy. For surface waves in the Earth, the group velocity is almost always lower than the phase velocity. Whereas phase velocity c = w/k, group velocity U = dw/dk.