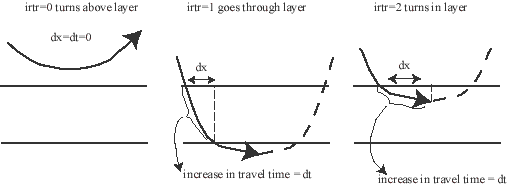
Step 2: Crustal phases.
It is often useful to think of seismic waves as rays. Technically, this is only justified when the wavelength of the wave is short compared to the velocity and amplitude gradients in the medium. You can read appendix 3 of your textbook if you are interested in why this is the case. When the velocity in a medium only changes as a function of depth, which to first order is the case in the Earth, each ray can be designated by a ray parameter. The ray parameter is constant along a ray. In a horizontally layered medium, the ray parameter, p, is given by:
p = sin(i)/v
= u sin(i)
where i is the angle that the ray makes with vertical and v is the velocity of the
medium. The slowness, u, is 1/v.
If there is a horizontal discontinuity between medium 1 and medium 2, the condition that p is constant
along the ray, is better known as Snell's law:
p1 = p2
u1 sin(i1) = u2 sin(i2)
At the turning depth of a ray (that is, where its propagation direction changes from downward to upward), the angle with the vertical, i, is 90 degrees. In that case:
p = utd
Thus, the ray with ray parameter p turns at the depth where the
velocity is 1/utd.
Consider the following model of the oceanic crust:
| Depth (km) | a (km/s) | b (km/s) | r (g/cc) |
| 0.0 | 4.50 | 2.40 | 2.0 |
| 1.5 | 6.80 | 3.75 | 2.8 |
| 6.0 | 7.00 | 3.85 | 2.9 |
| 6.5 | 8.00 | 4.60 | 3.1 |
| 10.0 | 8.10 | 4.70 | 3.1 |
Linear velocity gradients are assumed to exist at intermediate depths in the model.
1. At which depth does the P phase with p = 0.125 s/km turn? What is the ray
parameter of the S wave that turns at the same depth? What are the take-off angles of
both phases at the surface?
You will use Scilab again.
Start Scilab and change to your folder: chdir('Z:\yourname');
The function layerxt (in Y:\Intro_seismology2002\functions\Funlab2.sci) calculates the change in epicentral distance and travel time of a ray with ray
parameter p, traveling through a layer with thickness h (km), a slowness at the top,
utop, a slowness at the bottom, ubot, and a linear velocity gradient from top to bottom.
Figure 2 illustrates how this works.
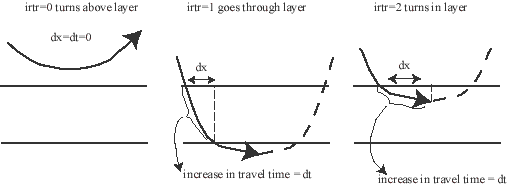
Figure 2. Illustration of function layerxt(p,h,utop,ubot). For each layer in a flat layered model, given a ray parameter p, three cases are possible, the ray has already turned above the layer (irtr=0), the ray goes through the layer (irtr=1), and the ray turns in the layer (irtr=2).
We have written a simple Scilab program around function layerxt to trace rays through the MARMOD model and produce P wave travel
times and epicentral distances using 100 values of p between 0.1235 and 0.2217 s/km. You can find it in Y:\Intro_seismology2002\raytracer.sci.
2. Copy the program to your directory and look at its contents. Try to describe
the program and understand how it works. Write a description in your report.
3. Run the program. The program produces plots of a) travel time T(X) plotted with a reduction velocity of 8 km/s, b)
distance as a function of ray parameter X(p), and c) tau(p) (= T(p) - pX(p) ). [to learn more about plotting with Scilab, try: help plot2d,
help xset, help xbasc, and help subplot].
On each plot, label Pg (the phase that only travels through the crust), PmP (the phase that is
'reflected' by the velocity gradient at the Moho), and Pn (the phase that also travels through the
mantle).
4. What is the cross-over distance (the closest distance at which Pn arrives before Pg)?
5. What is the reason that we plot T-X/8 vs. X, and not just T vs X? To see
the difference type: xbasc(); plot2d(X,T);
(6.) The triplication results from the velocity gradient that represents the Moho
discontinuity. Make the change from crust (7.0 km/s) to mantle (8.0 km/s) less abrupt by deleting the 4th
line in model MARMOD. In other words, instead of having four layers, the model now only has
three layers.
Run your script again. How does this change affect the triplication (give a detailed description)?
(7.) Add a line to your revised model MARMOD, at 3.5 km depth the P velocity is only 6.5
km/s, the S velocity is 3.70 km/s, and the density is 2.78 g/cc. Run the script
again. How does this slight low velocity zone affect T(X), X(p), and tau(p)?
8. MARMOD represents an oceanic crustal model. Consider a model called
CONTINENT that is similar to MARMOD except that the depth 1.5 km must be changed to 15 km,
6.0 km to 30 km, and 6.5 km to 30.5 km, and 10 km to 40 km. Change your program so that it
calculates X and T for model 'CONTINENT' instead of model 'MARMOD'. Run it. What is the
cross-over distance for this model?
top |
home |
next step |
lab 1. |
lab 2. |
lab 3. |
lab 4. |
lab 5.